平衡点が唯一,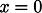 であるような非線形システム
であるような非線形システム
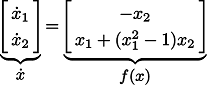
に対する正定値関数
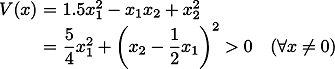
および 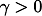 が与えられたとき,
が与えられたとき,
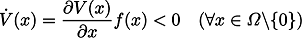
を満足するかどうかを調べる問題を考える.ただし,
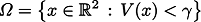
である.
この問題が可解であるための十分条件は,
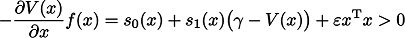
を書き換えた
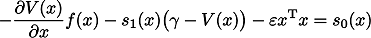
が二乗和多項式となるような,二乗和多項式 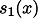 が存在することである.ただし,
が存在することである.ただし, は微小な正数である.
は微小な正数である.
たとえば,多項式 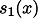 の次数を 2 とすると,
の次数を 2 とすると,
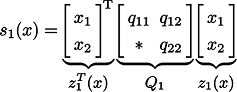
である.このとき,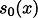 は4 次式となり,
は4 次式となり,
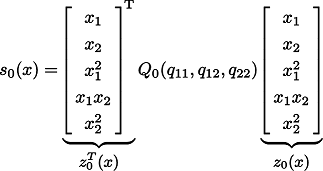
という形式で記述できる.したがって,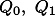 が半正定となる
が半正定となる 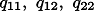 が見つかれば,この問題は可解である.
が見つかれば,この問題は可解である.
>> doa_analysis
-------------------------------------------------------------------------
YALMIP SOS module started...
-------------------------------------------------------------------------
Detected 3 parametric variables and 2 independent variables.
Detected 0 linear inequalities, 0 equality constraints and 0 LMIs.
Using kernel representation (options.sos.model=1).
Initially 3 monomials in R^2
Newton polytope (0 LPs).........Keeping 2 monomials (0.0468sec)
Finding symmetries..............Found 1 symmetry (0sec)
Partitioning using symmetry.....2x2(1)
Initially 6 monomials in R^2
Newton polytope (0 LPs).........Keeping 5 monomials (0sec)
Finding symmetries..............Found 1 symmetry (0.0312sec)
Partitioning using symmetry.....2x2(1) 3x3(1)
SeDuMi 1.3 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, theta = 0.250, beta = 0.500
Put 3 free variables in a quadratic cone
eqs m = 11, order n = 10, dim = 22, blocks = 5
nnz(A) = 27 + 0, nnz(ADA) = 121, nnz(L) = 66
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 3.10E+000 0.000
1 : -2.52E-001 9.04E-001 0.000 0.2922 0.9000 0.9000 1.59 1 1 1.8E+000
2 : -1.87E-002 2.14E-001 0.000 0.2366 0.9000 0.9000 2.40 1 1 5.5E-001
3 : -3.82E-004 4.82E-003 0.000 0.0225 0.9900 0.9900 1.28 1 1 1.3E-001
4 : -6.30E-009 1.14E-007 0.000 0.0000 1.0000 1.0000 1.01 1 1 2.2E-006
5 : -1.80E-015 2.61E-014 0.000 0.0000 1.0000 1.0000 1.00 1 1 4.0E-013
iter seconds digits c*x b*y
5 0.6 5.2 0.0000000000e+000 -1.8046740173e-015
|Ax-b| = 1.6e-014, [Ay-c]_+ = 1.5E-015, |x|= 2.1e+000, |y|= 2.4e-014
Detailed timing (sec)
Pre IPM Post
2.660E-001 5.150E-001 7.500E-002
Max-norms: ||b||=9.157663e-001, ||c|| = 0,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 1.37566.
sol =
yalmiptime: 2.2100
solvertime: 0.9410
info: 'No problems detected (SeDuMi-1.3)'
problem: 0
dimacs: [8.5188e-015 0 0 1.4639e-015 1.8047e-015 1.8047e-015]
monos =
[2x1 sdpvar] [5x1 sdpvar]
Q =
[2x2 double] [5x5 double]
resi =
1.0e-013 *
0.0777
0.2559
>> Q{1} %%% Q1
ans =
0.6969 0.0054
0.0054 0.6576
>> min(eig(Q{1})) %%% Q1 の最小固有値
ans =
0.6569
>> sdisplay(monos{1}) %%% z1(x)
ans =
'z1(2)'
'z1(1)'
>> s1x = monos{1}'*Q{1}*monos{1}; %%% s1(x) = z1(x)'*Q1*z1(x)
>> sdisplay(s1x)
0.6576*z1(1)^2+0.0107*z1(1)*z1(2)+0.6969*z1(2)^2
>> Q{2} %%% Q0
ans =
0.6969 -0.3431 -0.4758 0 0
-0.3431 0.6439 0.1792 0 0
-0.4758 0.1792 0.9864 0 0
0 0 0 0.3031 -0.0054
0 0 0 -0.0054 0.3424
>> min(eig(Q{2})) %%% Q0 の最小固有値
ans =
0.2451
>> sdisplay(monos{2}) %%% z0(x)
ans =
'z1(2)^2'
'z1(1)*z1(2)'
'z1(1)^2'
'z1(2)'
'z1(1)'
>> s0x = monos{2}'*Q{2}*monos{2}; %%% s0(x) = z0(x)'*Q0*z0(x)
>> sdisplay(s0x)
0.3424*z1(1)^2-0.0107*z1(1)*z1(2)+0.3031*z1(2)^2
+0.3585*z1(1)^3*z1(2)-0.3077*z1(1)^2*z1(2)^2
+0.9864*z1(1)^4-0.6862*z1(1)*z1(2)^3+0.6969*z1(2)^4
>> sdisplay((- jacobian(v,x)*f - s1x*(gam - v) - ep*z1'*z1) - s0x)
-1.3489e-014*z1(1)^2-9.9920e-016*z1(1)*z1(2)-1.4821e-014*z1(2)^2
+1.3878e-015*z1(1)^3*z1(2)-8.2157e-015*z1(1)^2*z1(2)^2
+1.7764e-015*z1(1)^4-5.5511e-015*z1(1)*z1(2)^3-5.5511e-016*z1(2)^4
>> sdisplay(clean(...
(- jacobian(v,x)*f - s1x*(gam - v) - ep*z1'*z1) - s0x, ...
1e-6)) %%% 1e-6 以下の係数は無視
0
![]() であるような非線形システム
であるような非線形システム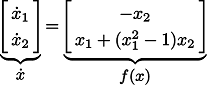
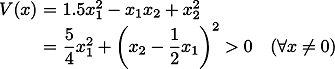
![]() が与えられたとき,
が与えられたとき,![]()
![]()
![]()
![]()
![]() が存在することである.ただし,
が存在することである.ただし,![]() は微小な正数である.
は微小な正数である.![]() の次数を 2 とすると,
の次数を 2 とすると,
![]() は4 次式となり,
は4 次式となり,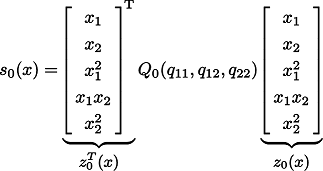
![]() が半正定となる
が半正定となる ![]() が見つかれば,この問題は可解である.
が見つかれば,この問題は可解である.